MONOID

Mathematikblatt für Mitdenkerinnen und Mitdenker

Errata

Leider schleichen sich immer mal wieder Fehler in die MONOID-Hefte ein.
Bitte schreibt uns eine E-Mail, sobald Ihr auch einen entdeckt. Vielen Dank.

Heft Nr. 157

• Auf S. 23 Mathespielerei I. Produktdastellung einer Zahlendifferenz

  Die Differenz, mit der die Zahl n definiert wurde, war aufgrund einer fehlenden Ziffer falsch. Die richtige Aufgabenstellung lautet:

  Es sei n = 112296² - 79896². Zeige, ohne n zu berechnen, dass gilt:

  Man kann n als Produkt der Zahlen 1, 2, 3, ..., 10, 11, 12, 13 schreiben.

  Die hier verfügbare PDF-Datei wurde korrigiert und enthält die korrekte Aufgabenstellung (17.03.2024).

Heft Nr. 152

• Fehler in Aufgabenstellung 1312

  Leider hat sich in die Aufgabenstellung der Neuen Aufgabe 1312 (Heft 152, S. 26) ein Fehler eingeschlichen. Es muss dort heißen: "Wenn Tatjana als Erste die Kugel wirft, wie groß ist dann die Wahrscheinlichkeit..."

  Wir bitten den Fehler zu entschuldigen und wünschen trotzdem viel Spaß und Erfolg beim Knobeln.

Heft Nr. 151

• Kleiner Fehler

  Leider war die Aufgabenstellung der Aufgabe 1309 in Heft 151 unvollständig und somit die Aufgabe nicht lösbar. Die korrekte Aufgabenstellung lautet:

  Gegeben sei ein rechtwinkligen Dreieck ABC mit den Seitenlängen a=20, b=15 und c=25. Ferner sei D der Höhenfußpunkt der Höhe auf die Seite c. Bestimme die Flächeninhalte der Dreiecke ADC und DBC.

Heft Nr. 144

• Lösung der Neuen Aufgabe 1279: Zahlen gesucht
  In Heft 144 wird als die Lösung für Aufgabe 1279 aus Heft Nr. 143 nur a=51 und b=30 angegeben. Weitere Lösungen sind aber auch a=52 und b=29 sowie a=50 und b=31.
  

Heft Nr. 142

• Divergenz der Reihe aus den Kehrwerten der Primzahlen
  Auf Seite 32 fehlen die Summanden, korrekt muss es heißen:
  
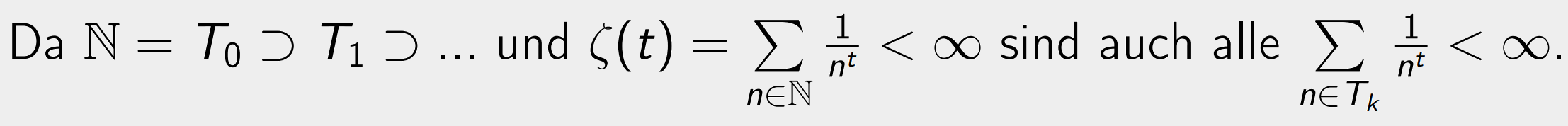  Außerdem wurden die Mengenzeichen ℕ der natürlichen Zahlen nicht richtig dargestellt.

Heft Nr. 141

• Mathespielerei: II. Ein magischer quadratischer Ring
  Die Aufgabenstellung muss wie folgt lauten:
  Fülle die leeren Felder so mit Zahlen zwischen 16 und 23, dass die Summe jeder Seite des Quadrats gleich ist.

Heft Nr. 140

• Aufgaben aus dem Neuen Jahr: Rationale Zahlen aufsummiert
  Die Aufgabenstellung muss wie folgt lauten:
  Bestimme die Summe S aller positiven Brüche < 1, deren Nenner ≤ 2020 ist.
• Aufgaben aus dem Neuen Jahr: Wahr oder falsch
  Die Aufgabenstellung muss wie folgt lauten:
  1∙2 + 2∙3 + 3∙4 + … + 2017∙2018 + 2018∙2019 + 2019∙2020 =
  2(1∙2019 + 2∙2018 + 3∙2017 + … + 2018∙2 + 2019∙1)?

Heft Nr. 135

• Text: Was uns über den Weg gelaufen ist
  Die Aufgabenstellung muss wie folgt lauten:
  Wenn man die links und rechts stehenden Ziffern spaltenweise addiert, erhält man die Ziffern zweier 10-stelligen Zahlen. Welche davon ist größer?

Heft Nr. 133

• Mathespielerei: Aufgabe 1
  Man streiche in der vorletzten Zeile die Worte 'die Summe'. Dann sollte die Aufgabenstellung sinnvoll sein.

Heft Nr. 131

• Aufgabe für den Computerfan
  Es fehlt eine Print-Anweisung ganz am Schluss.
• Musterlösung von Aufgabe 3
  10^255-1 hat 225 mal die Ziffer 9

Heft Nr. 130

• Mathespielerei: Eine lange Rechnung
  Hier stimmt die Aufgabenstellung leider nicht. Richtig lautet die Aufgabe:
  Die Summe von zwei aufeinanderfolgenden natürlichen Zahlen x und x+1 wird mit 17 multipliziert. Danach addieren wir 213, dann dividieren wir durch 4,
  subtrahieren dann 9, multiplizieren mit 15 und subtrahieren zuletzt 254. Das Ergebnis ist 1111. Finde x.

Heft Nr. 129

• Die Aufgabe für den Computerfan
  Hier stimmt die Definition der Kimberling-Folge leider nicht. Statt einem a muss dort eine 1 stehen.

Heft Nr. 126

• In Heft 126 (März 2016) waren leider falsche Zahlen in der Aufgabe für den Computerfan angegeben.
  Wegen dieses Fehlers ist nun die Abgabefrist dieser Aufgabe der 15.10.2016. Unten finden Sie die verbesserte Version der Aufgabe. Die alten, falschen Zahlen stehen in Klammern:
  
  "WG-CRAPS" ist eine Variante des Spiels "CRAPS" mit folgenden Spielregeln: Ein Spieler würfelt mit zwei idealen Würfeln. Wirft der Spieler im ersten Wurf die Augensumme 7 oder 10 (4), so gewinnt er sofort. Wirft er 2, 3 (11) oder 12, so ist dies ein "Crap" und er verliert sofort. Wirft er eine der Augensummen 4, (3), 5, 6, 8, 9 oder 11 (10), so ist die Augensumme sein "Point" und er würfelt ein weiteres Mal. Ab dem zweiten Wurf gilt nun: Wirft der Spieler seinen "Point", so gewinnt er. Wirft er die Augensumme 7, so verliert er. Wirft er irgendeine andere Augensumme, so würfelt er erneut.
  
  Zeige mit einem Simulationsprogramm, dass "WG-CRAPS" (im Gegensatz zum "Original-CRAPS") fair ist! Dabei nennen wir ein Spiel fair (aus Sicht des Spielers), wenn die Gewinnwahrscheinlichkeit größer gleich 50% ist. Zusatzpunkte erhälst du, wenn du mit einem geeigneten Konfidenz-Intervall dein Simulationsergebnis bestätigst. Das Signifikanz-Niveau etc. ist dir freigestellt. (W.G.)
  
  Hinweis: Ihr könnt Eure Lösungen bis zum 15. Oktober 2016 einschicken; denn auch hierbei gibt es Punkte zu ergattern, die bei der Vergabe des Forscherpreises eingehen. Ein eigenes Programm solltet Ihr als Textdatei und die EXE-Datei am besten "gezippt" als E-Mail-Anhang an monoid@mathematik.uni-mainz.de einsenden. Die Lösungen werden im übernächsten Heft erscheinen.

Heft Nr. 124

• In Heft 124 (Dez. 2015) wurde (63, 16, 65) als Beispiel für ein pythagoreisches Tripel (63^2+16^2=65^2) angegeben, für das keine ganzzahligen k, m, n existieren würden mit:
  63=k(m^2-n^2)
  16=2kmn
  65=k(m^2+n^2)
  Für k=1, m=8, n=1 gilt aber:
  63=8^2-1^2
  16=2*8*1
  65=8^2+1^2
  Im abgedruckten Beweis fehlt S.31, 6. Zeile von oben, die Zerlegung "65=1+64". Die Redaktion bedankt sich sehr herzlich bei Herrn Frank Rehm, der uns auf den Fehler aufmerksam gemacht hat und entschuldigt sich bei allen Löesern!

Heft Nr. 121

• Neue Aufgabe 1126: Teiler einer Primzahlen-Summe
  Hier stimmt die Aufgabenstellung leider nicht. Richtig lautet die Aufgabe:
  Zeige: Für zwei unmittelbar aufeinander folgende Primzahlen p und q, beide > 2, gilt: p + q ist eine Zahl,
  deren Zerlegung mindestens drei Primfaktoren enthält, die nicht notwendigerweise verschieden sein müssen.

Heft Nr. 120

• Neue Aufgabe 1113: Bunt gefärbte Strecken
  Hier stimmt in der Aufgabenstellung die Anzahl der farbigen Strecken nicht. Es sollten eigentlich 2 029 105 solcher Strecken sein.

Heft Nr. 117

• Lösung zur Aufgabe 1091: Ein Näherungsverfahren für Wurzel n
  Korrigierte Lösung
• Auf Seite 38 muss in der letzten Zeile des Pascalschen Dreiecks die vorletzte Zahl eine 6 und keine 5 sein.
• Auf Seite 39 muss es heißen: Die Menge aller natürlichen Zahlen <= n.
• Auf Seite 41: Gauß wurde im Jahr 1777 geboren.

Heft Nr. 116

• Neue Aufgabe 1090: Regelmäßiges Achteck im Quadrat
  Die Angabe über das Achteck ist leider nicht korrekt, es ist NICHT regelmäßig.
  
• Rubrik der Löser und Löserinnen
  Der Stand der Punkte ist hier falsch. Richtig ist, dass die Punkte bis einschließlich Heft 114 berücksichtigt wurden.

Heft Nr. 112

• Aufgabe 1061: Quadrat im Dreieck
  In der dritten Zeile ist das D falsch. Richtig ist: "..., dass die Seite EF des Quadrats auf der Seite AB und die Endpunkte
  G und H auf den Seiten BC und AC liegen".
  
• Der Kreis des Apollonios
  Der gute Apollonios ist uns ein bisschen zu alt geraten. Er lebte in Wirklichkeit um 260 v.Chr. bis 190 v.Chr. in Alexandria.

Heft Nr. 107

• Wir bitten Iolanthe Köcher um Entschuldigung - leider ist über ihre abgedruckte Musterlösung zur Fußballaufgabe
  aus den Mathespielereien von Heft 106 eine ganze Horde von Rechtschreibfehlern hergefallen, die im Original nicht
  vorhanden waren. Wir bestellen für das nächste Heft einen besseren Kammerjäger!

Heft Nr. 106

• Auf Seite 8 muss in Zeile 8 für die obere Schranke für L gelten: L < 1/n · π²/6 und in Zeile 9 geht,
  wenn man n gegen ∞ laufen lässt, 1/n · π²/6 gegen 0.
• In der Rubrik "Wer forscht mit?" (ab S. 33) lautet die Aufgabe auf S. 37 in Zeile 9 richtig:
  Man zeige, dass dann jede der Augenzahlen von 1 bis 5 mit Wahrscheinlichkeit 1/5 auftritt.

Heft Nr. 103

• Auf Seite 7 muss in Formel (6) in der dritten Zeile als Ergebnis 0,4914 stehen: gemäß der Spielerfahrung des Chevaliers eine
  Gewinnwahrscheinlichkeit < 0,5.

Heft Nr. 101

• Aufgabe 982: Falsche Freunde (wie sicher ist die PIN?)
  Bei der Lösung zu Aufgabenteil d) hat sich ein Fehler eingeschlichen: 10 · 9 · 4 ist natürlich 360,
  also lautet die korrekte Lösung: 3/360 ≈ 0,0083.
  
  
• Aufgabe 984: Spareinlage
  Die im Heft 101 abgedruckte Lösung, die nicht vom Aufgabensteller stammt, ist falsch. Die korrekte Lösung lautet:
• (a) Nach der Verzinsung für 2009 beträgt das Guthaben
  0,01€ · 1,03^2009+81 = 0,01€ · 1,03²⁰⁹⁰ ≈ 6,758 · 10²⁴€.
  Das sind fast 6,8 Quadrillion Euro (oder 6,8 Yotta-Euro).
• (b) Zum Zeitpunkt, da Caesar Millionär wird, gilt
  0,01€ · 1,03ⁿ⁺⁸¹ = 10⁶€, resp. 10⁸ = 10⁶€/0,01€ = 1,03ⁿ⁺⁸¹.
  Nach dem Übergang zum Logarithmus folgt
  lg(10⁸) = lg(1,03ⁿ⁺⁸¹) = (n+81) · lg(1,03).
  Damit ist n = (lg(10⁸) : lg(1,03)) - 81 ≈ 623,2 - 81 = 542,2 und nach der Verzinsung
  am 31. Dezember 543 wäre Caesar Millionär.
• (c) Abgesehen von Währungsreformen, Inflation und der Tatsache, dass es zu Caesars Zeit noch nicht den Euro gab:
  Die Zinsgutschriften werden von den Banken gerundet, das heißt nach der ersten Verzinsung ergäbe sich zwar
  theoretisch ein Kapital von 0,01€ · 1,03 = 0,0103€, aber wegen der Rundung
  würde es bei 0,01e bleiben ? und das setzt sich ewig so fort. (MG)


• Aufgabe 986: Wanderer
  Hier fehlte die Lösung zu Aufgabenteil b), die hier nachgereicht wird:
  Für die Gesamtstrecke s = |AC| benötigt der Fußgänger die Zeit t = s : v, der Radfahrer ohne
  Ruhepause T = s : V = s : (a · v), mit Berücksichtigung der Ruhepause R = 20 min, also t = T + R.
  Es ist also s : v = (s : V) + R und somit s = (Rva) : (a-1) für die Gesamtstrecke und t = s : v = Ra : (a-1) für die benötigte Zeit.

Heft Nr. 97

• Auf Seite 7 muss die Formel (1) folgendermaßen lauten:
  π/4 = 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...
  Andernfalls ergibt das Produkt auf der rechten Seite: 3/4 * π.
• Auf Seite 11 muss in der dritten Zeile unterhalb der Formulierung (4)
  n₄ > n₅ > n₆ > n₇ > ?
  stehen und in der fünften bzw. sechsten Zeile unterhalb (4) entsprechend
  n₁ > n₂ > n₃ > n₄ > ?

Heft Nr. 92

• Im Artikel „Die besondere Augabe: Eingeschränkter Flugverkehr" ist ein Argument etwas ungenau. In den Überlegungen
  des Hof-Mathematicus, Teil (a) muss es im letzten Absatz heißen (Seite 9):
  Da es ungeradzahlig viele Städte gibt, müssen die Fallunterscheidungen damit enden, dass man wie im ersten Fall auf
  eine Stadt S_m mit dem größten e_m stößt -- in S_m landet daher kein Flugzeug.
• Albert Einstein wurde am 14.03.1879 geboren.

Heft Nr. 90

• In der Aufgabenstellung auf der Seite für den Computerfan (Seite 15) lautet die kp-Lösung zum ersten Beispiel (19,6).

Heft Nr. 89

• In der Aufgabenstellung zur "Neuen Aufgabe" 907 muss es anstatt z=ababa(a+b)b heißen z=ab0aba(a+b)b.

Heft Nr. 85

• In der "Neuen Aufgabe" sollen die 3x3-Quadrate nur fast-magische Quadrate sein, das heißt jede Zeile und jede Spalte
  hat die gleiche Summe. Dies gilt aber entgegen der Aufgabenstellung nicht für die Diagonale.
  Die Bedingung (2) soll auch weiterhin gelten.

Heft Nr. 83

• Im "Aufzugs-Problem" auf Seite 18 muss man für das dritte Stockwerk zwei Fälle unterscheiden, je nachdem,
  ob 8 oder 9 Weiterfahrende aus dem zweiten Stock ankamen. Daraus ergibt sich die Anzahl der Weiterfahrenden
  im dritten Stock zu 9, im vierten Stock zu 10, im fünften zu 12 und schließlich im sechsten
  zu 14 bzw. 15. Somit ist die korrekte Antwort auf Frage a): Im dritten Stock steigen möglicher Weise
  drei Personen aus und drei ein. Frage b):
  Im sechsten Stock
  befinden sich mit Sicherheit mehr Leute im Lift als im Erdgeschoss eingestiegen sind.
• In der zweiten Lösung zu "Punkte und 9 Strecken" auf Seite 20 oben rechts ist eine Strecke falsch eingetragen.
  Richtig soll die Figur so aussehen:
  
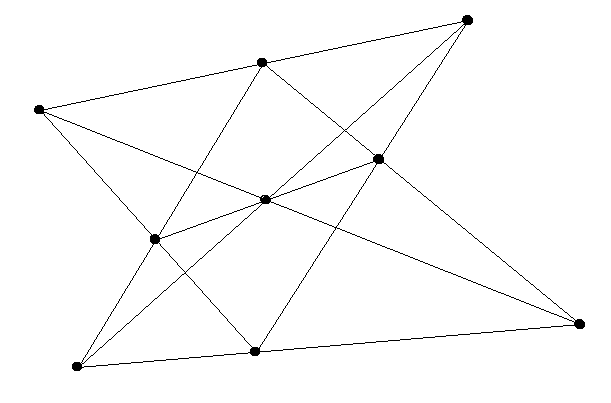
• In der Aufgabe "Winkel im Parallelogramm" auf Seite 20 muss der Winkel PQR durch Winkel RQP ersetzt werden.
  (Grund: Die Orientierung von Winkeln erfolgt im mathematisch positiven Sinne, also gegen den Uhrzeigersinn.)
  
• Ein Würfel hat nicht drei, sondern vier Raumdiagonalen; in der Zeichnung S. 22, "Ein an Diagonalen
  armer Körper" ist also noch eine Raumdiagonale einzutragen.
• Auf Seite 9 ist im Absatz (2) der Klammereinschub (nicht aber Grenzpunkt) zu ersetzen durch
  (nicht aber durch einen Schnittpunkt von Grenzlinien).
• Auf S. 15 muss es in der 2. Zeile vor dem unteren Quadrat (26)² statt 6² beziehungsweise
  (2n)² statt n² heißen.

Heft Nr. 81

• In der Aufgabe 846 'Gemeinsame Nullstellen' wurde die Funktion g(x) falsch angegeben. Sie sollte eigentlich
  g(x)=ax³+(13a-3a²)x² -(39a²+30a)x+90a² heißen.
  Auf diese Funktion passt dann auch die in Heft 81 wiedergegebene Lösung.
  
  Dagegen lautet die Lösung für die Aufgabe, wie sie in Heft 80 gestellt und in Heft 81 wiederholt wurde:
  Die Funktion f hat die Nullstellen 2 und -15 (z.B. mit p-q-Formel). Setzen wir 2 in g(x) ein und bestimmen a aus
  g(2)=0, so ergibt sich a=0 oder a=91/51.
  Für a=0 ist g das Nullpolynom, das ganz R als Nullstellenmenge hat und sicher nicht in Betracht kommt.
  Für a=91/51 ist jedoch g(-15)=-118300/17 und
  somit nicht 0.
  Man kann also a nicht so wählen, dass die Nullstellenmengen von f und g übereinstimmen.

Heft Nr. 80

• Leider sind im Heft 80 die Lebensdaten des polnischen Mathematikers Waclaw Sierpinski nicht korrekt
  wiedergegeben worden; richtig ist: 1882-1969.

Heft Nr. 74

• Auf Seite 7 muss die Angabe der Lebensdaten von G. Cramer korrekt lauten: 1704 - 1752.

Heft Nr. 73

• Auf Seite 3 muss der mittlere Abschnitt lauten:
  Lösung:
  Am Anfang des 1. Monats haben wir 1 Paar.
  Am Anfang des 2. Monats haben wir immer noch nur dieses 1 Paar (a₁).
  Am Anfang des 3. Monats haben wir 1 neugeb. Paar, also insgesamt 2=1+1 Paare (a₂).
  Am Anfang des 4. Monats haben wir wieder 1 neugeb. Paar, also insgesamt 3=2+1 Paare (a₃).
  Am Anfang des 5. Monats haben wir 2 neugeb. Paare, also insgesamt 5=3+2 Paare (a₄).
  Am Anfang des 6. Monats haben wir 3 neugeb. Paare, also insgesamt 8=5+3 Paare (a₅).
  So fortfahrend erhalten wir die Folge:
  1 (Anfang 1. Monat), 1 (Anfang 2. Monat), 2 (Anfang 3. Monat), 3, 5, 8, 13, 21, 34, 55, 89, 144
  (Anfang 12. Monat, d.h. Ende des Jahres).
  Antwort:
  Am Ende des Jahres haben wir a₁₁ = 144 Kaninchen.
• Auf Seite 5 muss die 6.-letzte Zeile lauten:
  Für eine Zahl n mit k Primfaktoren, n=p₁^a₁   p₂^a₂   p₃^a₃   . . .   p_k^a_k ist die Anzahl der Teiler:
  A(n) = (a₁ + 1) (a₂ + 1) . . . (a_k + 1).

Heft Nr. 72

• Auf Seite 30 sehen die Ungleichungen (2) richtig so aus:
  a² > b² + c², b²> a² + c² oder c² > a² + b².

Heft Nr. 70

• Auf S. 19 muss bei den Neuen Mathespielereien in der Aufgabe Fremdsprachen im Aufgabentext das
  Wörtchen 'nur' zweimal gestrichen werden.
  Es muss also heißen: '... 18 Kinder sprechen Französisch und 17 Englisch.'

Heft Nr. 69

• Auf Seite 19 ("Neue Mathespielereien") muss es in der Aufgabe "Das Glückskind" heißen:
  ...und viermal hintereinander hat er seinen Einsatz verdreifacht.
• Die Folien des Vortrags von Prof. Dr. D. van Straten Über das Unendliche anläßlich der Preisvergabefeier sind zu finden unter:
  http://www2.Mathematik.Uni-Mainz.DE/~straten/publics/vortragUnendlich/vortrag.php.
• Auf S. 10 muss es unter (b), (c) und (d) der Aufgabenstellung (*) statt (3) heißen.
• Auf S. 25, Lösung zu Aufgabe 767: Während Gleichung (1) mit 100 multipliziert wird, muss Gleichung (2) natürlich mit
  100^3=10^6 multipliziert werden.
  Außerdem muss es in Zeile 6 von unten v statt u heißen.

Heft Nr. 67

• Auf Seite 31 muß die Formel in der oberen Hälfte der Seite natürlich lauten:
  (a*b)*c = a*(b*c) (die Multiplikation ist assoziativ).

Heft Nr. 65

• Die korrekte URL zur Aufgabe mit dem Gefangenendilemma lautet:
  http://www.informatik.uni-mainz.de/~astra/schueler/dilemma.html.
• Seite 11, Lösung zu Aufgabe 2: in der 3. Zeile sollte k Element der natürlichen Zahlen stehen.
• Auf den Seiten 19, 23 und 24 sind Es statt der beabsichtigten Multiplikationspunkte aufgetaucht.

| Impressum | E-Mail an MONOID | Institut für Mathematik der Universität Mainz | Datenschutz |