MONOID

Mathematikblatt für Mitdenkerinnen und Mitdenker

MONOID 68 - Aufgaben

Zwei Aufgaben aus dem Heft Nummer 68, je eine aus den Mathespielereien (für die Klassen 5-7) und eine für die Klassen 8-13. Weitere Aufgaben und Artikel zu mathematischen Themen enthält das aktuelle Heft (für Bestellungen siehe Kontakt). Für eingesandte Lösungen gibt es Punkte und am Ende des Jahres winken Preise!

Dreieckszerlegung

Gegeben ist ein Dreieck ABC mit verschieden langen Seiten a,b,c. Konstruiere auf der Seite AB einen Punkt D, so dass die Verbindungsstrecke CD das Dreieck ABC in zwei umfangsgleiche Teildreiecke ADC, BCD zerlegt. Wie lang ist die Strecke AD?

In der Aufgabe wird eine allgemeine Formel gefragt. Hier möchten wir aber nur die Lösung für zwei Beispiele wissen:

In die Liste der LöserInnen können sich all jene eintragen, die eine Lösung gefunden und mit obigem Formular überprüft haben.

Aufgabe 765 (Gemälde-Ausstellung)

Für die Gemälde der modernen Künstlerin Ursula Molinera soll ein eigenes Ausstellungsgebäude errichtet werden. Dabei soll jede der insgesamt 14 Stilepochen der Künstlerin auf einer eigenen Ausstellungswand dokumentiert werden. Der vorgesehene Leiter der Einrichtung, Dr. Eric Lindon, will die Ausstellung durch eine Videokamera in der Mitte des Gebäudes überwachen lassen, nachdem er erfahren hat, dass das Gebäude aus einem einzigen Raum bestehen wird. Arthur Forrester, ein Freund des mit dem Bau beauftragten Architekten, macht ihn darauf aufmerksam, dass dies bei unkonventioneller Gestaltung des Raums möglicherweise nicht ausreicht, z.B. schon bei einem Raum mit nur sechs Wänden wie dem in der Skizze unten wären mindestens zwei Kameras erforderlich.

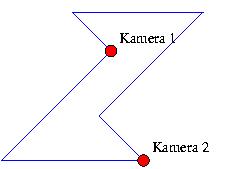
Wie viele Kameras muss man vorsehen, damit bei 14 Wänden auf jeden Fall der ganze Raum kontrollierbar ist? Was ist die allgemeine Lösung bei n Wänden?
Bemerkung: Wir nehmen an, dass eine Videokamera nach allen Seiten 'sieht' und dass es keine Säulen oder Ähnliches gibt, die die Sicht versperren.

In der Aufgabe wird eine allgemeine Formel gefragt. Hier möchten wir aber nur die Lösung für zwei Beispiele wissen:

In die Liste der LöserInnen können sich all jene eintragen, die eine Lösung gefunden und mit obigem Formular überprüft haben.

| Impressum | E-Mail an MONOID | Institut für Mathematik der Universität Mainz | Datenschutz |